Unlocking the Universe: How to Find the Sides of Any Triangle
Have you ever gazed at a majestic mountain range or a towering skyscraper and wondered how we measure such colossal structures? Or perhaps you've been captivated by the intricate geometry of a honeycomb or the delicate symmetry of a snowflake. These natural and man-made wonders share a common thread: their underlying structure can be understood through the elegant principles of triangles and the powerful tool of trigonometry.
Trigonometry, often considered a cornerstone of mathematics, empowers us to unravel the mysteries of triangles and their applications in various fields. It provides a unique lens through which we can analyze and comprehend the relationships between angles and sides in right triangles, opening up a world of possibilities for measurement and calculation.
At its core, trigonometry for determining the lengths of triangle sides centers around three fundamental trigonometric ratios: sine (sin), cosine (cos), and tangent (tan). These ratios, defined as ratios between the lengths of two sides of a right triangle, provide a powerful framework for solving for unknown sides given an angle and one side length.
The historical roots of trigonometry can be traced back to ancient civilizations like the Babylonians and Egyptians, who employed rudimentary forms of trigonometry for astronomical calculations and land surveying. The Greeks, particularly Hipparchus and Ptolemy, made significant strides in formalizing trigonometric concepts and developing trigonometric tables. Over the centuries, mathematicians like Aryabhata in India and Al-Khwarizmi in Persia further refined these concepts, laying the foundation for the sophisticated trigonometric tools we use today.
The significance of trigonometry extends far beyond the realm of theoretical mathematics. Its applications permeate various fields, including architecture, engineering, physics, astronomy, navigation, and even music. From calculating the height of a building using the angle of elevation and a known distance to determining the trajectory of a projectile based on its launch angle and velocity, trigonometry provides the essential tools for solving real-world problems.
To illustrate the power of trigonometry, imagine you're an architect tasked with designing a ramp for a building. You know the desired angle of incline for the ramp and the vertical height it needs to cover. Using trigonometry, you can easily calculate the required length of the ramp, ensuring it meets accessibility standards while seamlessly integrating with the building's design.
In another scenario, consider a surveyor tasked with determining the distance across a river. By measuring a baseline distance along one bank and using a theodolite to measure the angles between the baseline and a point on the opposite bank, the surveyor can leverage trigonometric principles to accurately calculate the river's width.
Advantages and Disadvantages of Using Trigonometry to Solve for Sides
| Advantages | Disadvantages |
|---|---|
| Provides accurate solutions for right triangles | Limited to right triangles; cannot be directly applied to oblique triangles |
| Widely applicable in various fields, including engineering, physics, and architecture | Requires knowledge of trigonometric ratios and their relationships |
| Simplifies complex geometric problems by relating angles and sides | Potential for errors in measurement or rounding can impact the accuracy of results |
Mastering the art of trigonometry for solving the lengths of triangle sides empowers individuals with a versatile tool applicable to a wide range of disciplines. Whether you're a student, a professional, or simply someone who appreciates the beauty and utility of mathematics, understanding trigonometry opens up a world of possibilities for exploration and problem-solving.
Saying i do again renewing vows and legalities of remarrying your husband in indonesia
Fuel your adventures mastering the art of refilling camping propane bottles
St lucie county real estate taxes decoding the sunshine states levy

trigonometry solving for sides | Solidarios Con Garzon

Triangle Similarity Real Life Problems at Katherine Granger blog | Solidarios Con Garzon

trigonometry solving for sides | Solidarios Con Garzon

trigonometry solving for sides | Solidarios Con Garzon

trigonometry solving for sides | Solidarios Con Garzon

trigonometry solving for sides | Solidarios Con Garzon

Labelling Right Angled Triangles Worksheet | Solidarios Con Garzon
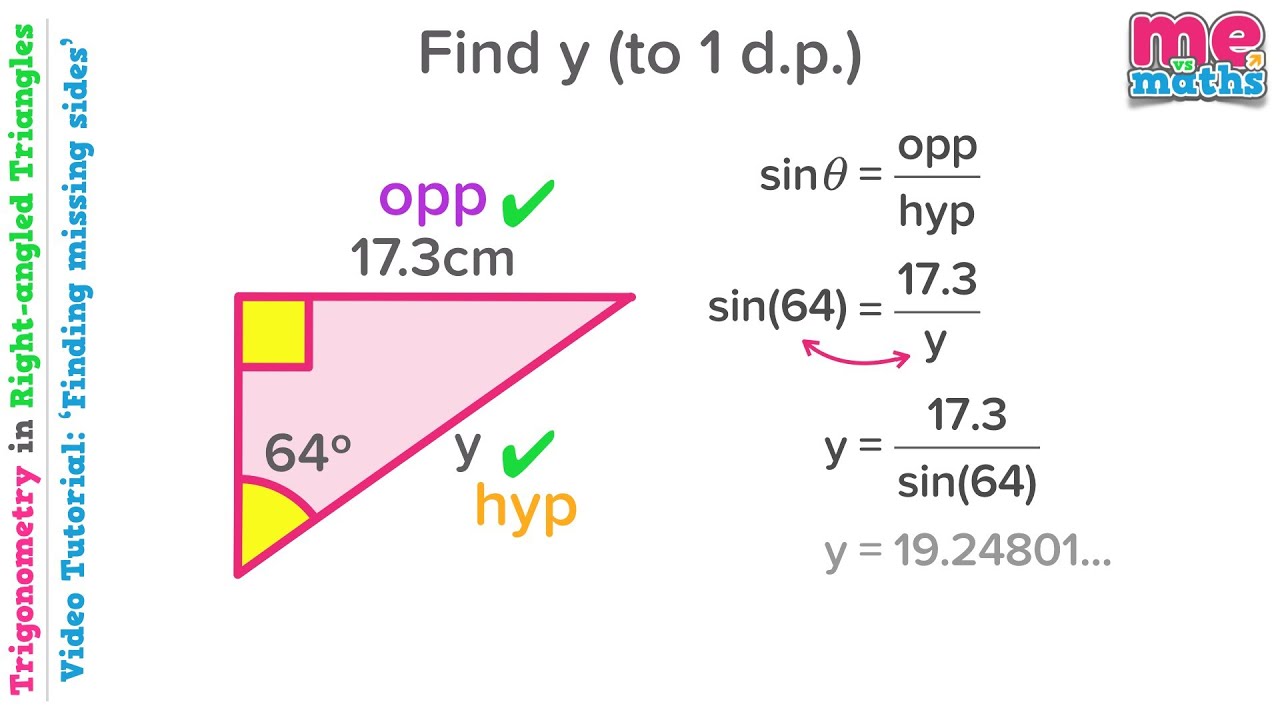
trigonometry solving for sides | Solidarios Con Garzon

trigonometry solving for sides | Solidarios Con Garzon

trigonometry solving for sides | Solidarios Con Garzon

Geometry Trig Word Problems Worksheet Answers | Solidarios Con Garzon

Trig angle cheat sheet | Solidarios Con Garzon

trigonometry solving for sides | Solidarios Con Garzon

trigonometry solving for sides | Solidarios Con Garzon

trigonometry solving for sides | Solidarios Con Garzon