The Subtle Art of Adding and Subtracting Fractions: A Journey Through Numerical Harmony
From the ancient Egyptians meticulously measuring land to modern-day bakers perfecting their recipes, fractions have woven themselves into the fabric of human understanding. The act of combining and comparing parts of a whole – the essence of fraction addition and subtraction – represents a fundamental step in our journey to quantify the world around us. But beyond their practical utility, these operations whisper a deeper story about the delicate balance and interconnectedness of things.
Imagine a world without fractions. Could we accurately share resources, build structures with precision, or understand the rhythms of the natural world? The answer, resoundingly, is no. Fraction operations, particularly addition and subtracting fractions, are not mere mathematical procedures; they are essential tools for understanding proportions, ratios, and the delicate dance between parts and wholes. They empower us to express quantities that fall between whole numbers, opening up a universe of nuance and precision.
The history of fractions is intertwined with the development of mathematics itself. Ancient civilizations grappled with the concept of representing parts of a whole, leading to the development of various systems for expressing fractional quantities. The Egyptians, for instance, primarily used unit fractions, where the numerator is always one. The Babylonians, on the other hand, employed a sexagesimal system (base-60), which is still reflected in our modern timekeeping. These early systems laid the groundwork for our current understanding of fractions and their operations.
Adding and subtracting fractions presents a unique challenge: unlike whole numbers, which can be directly combined or separated, fractions require a common language – a shared denominator. This need for a common ground highlights a profound mathematical truth: comparison and combination require a shared framework. This principle resonates far beyond the realm of fractions, influencing fields like statistics, economics, and even social sciences.
Before diving into the practicalities of fraction addition and subtraction, it’s crucial to grasp the basic terminology. A fraction represents a part of a whole. It consists of a numerator (the top number) indicating the number of parts we have and a denominator (the bottom number) indicating the total number of equal parts that make up the whole. For example, in the fraction 3/5, 3 is the numerator, and 5 is the denominator.
To add or subtract fractions with the same denominator, simply add or subtract the numerators and keep the denominator the same. For instance, 2/7 + 3/7 = 5/7. If the denominators are different, we first need to find a common denominator, usually the least common multiple (LCM) of the original denominators. Then, we convert each fraction to an equivalent fraction with the common denominator. Once the fractions share a common denominator, we can add or subtract the numerators as before.
One benefit of understanding fraction addition and subtraction is its practical application in everyday life. Imagine baking a cake. The recipe might call for 1/2 cup of sugar and 1/4 cup of butter. To determine the total amount of these ingredients, you need to add the fractions.
Another benefit lies in its crucial role in other fields of mathematics. Algebra, calculus, and statistics all build upon the foundations of fraction operations. Mastering these skills early on sets the stage for future success in more advanced mathematical pursuits.
Further, understanding fractions fosters critical thinking skills. The process of finding common denominators, simplifying fractions, and reasoning about proportions strengthens problem-solving abilities that extend beyond mathematics.
Advantages and Disadvantages of Working with Fractions
| Advantages | Disadvantages |
|---|---|
| Precision in representing quantities | Can be complex to work with compared to whole numbers |
| Foundation for advanced math concepts | Require understanding of concepts like least common multiple |
| Practical application in everyday life | Potential for errors when converting to common denominators |
Best Practices:
1. Always simplify your final answer. Reduce the fraction to its lowest terms.
2. Double-check your common denominator. Make sure it is indeed the least common multiple.
3. Convert mixed numbers to improper fractions before adding or subtracting.
4. Visualize the fractions. Drawing diagrams can help understand the process.
5. Practice regularly. The more you work with fractions, the more comfortable you will become.
Real-world Examples:
1. Combining ingredients in a recipe.
2. Calculating discounts at a store.
3. Measuring lengths of wood for a project.
4. Dividing pizza slices equally.
5. Determining the total time spent on various tasks.
Challenges and Solutions:
1. Finding common denominators for large numbers. Solution: Use prime factorization.
2. Dealing with mixed numbers. Solution: Convert to improper fractions.
3. Subtracting fractions with different denominators. Solution: Find the least common denominator.
4. Simplifying complex fractions. Solution: Factor the numerator and denominator.
5. Understanding the concept of equivalent fractions. Solution: Use visual aids like pie charts.
Frequently Asked Questions:
1. What is a fraction? Answer: A part of a whole.
2. What is a numerator? Answer: The top number in a fraction.
3. What is a denominator? Answer: The bottom number in a fraction.
4. How do you add fractions with the same denominator? Answer: Add the numerators, keep the denominator the same.
5. How do you subtract fractions with different denominators? Answer: Find a common denominator, convert the fractions, then subtract the numerators.
6. What is the least common multiple (LCM)? Answer: The smallest multiple that two or more numbers share.
7. How do you simplify a fraction? Answer: Divide the numerator and denominator by their greatest common factor (GCF).
8. What is an improper fraction? Answer: A fraction where the numerator is greater than or equal to the denominator.
Tips and Tricks:
Use visual aids to understand the concept better. Draw diagrams or use manipulatives to represent fractions.
In conclusion, the art of fraction addition and subtraction stands as a testament to humanity's pursuit of precision and understanding. From its ancient origins to its modern applications, the ability to combine and compare parts of a whole has empowered us to navigate a complex world. Mastering these fundamental operations is not just about memorizing procedures; it's about developing a deep appreciation for the interconnectedness of quantities and the delicate balance between parts and wholes. By embracing the challenges and exploring the intricacies of fraction addition and subtraction, we unlock a deeper understanding of mathematics and its profound impact on our lives. So, embark on this numerical journey, explore the rich history, practice the techniques, and discover the power of fractions to unlock a world of mathematical harmony. As you delve deeper into this fascinating world, you'll find that the ability to add and subtract fractions is not just a mathematical skill, but a key to unlocking a deeper understanding of the universe around us.
Finding your path exploring rehabilitation options in santa rosa county
Knockout nostalgia diving deep into the punch out arcade experience
Unlock the power of stick figures printable from doodles to diagrams
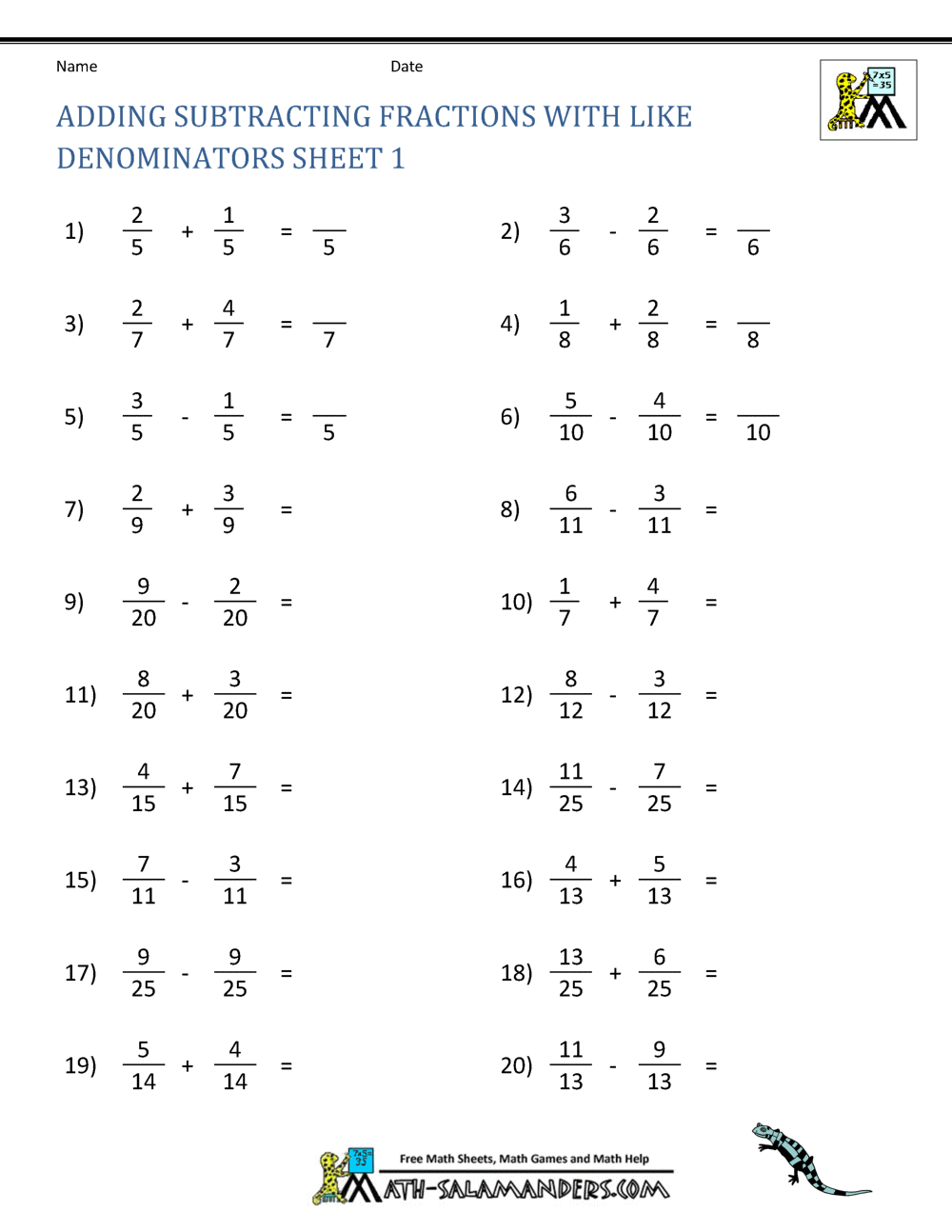
Fraction Worksheet Addition And Subtraction | Solidarios Con Garzon

How To Adding Fractions | Solidarios Con Garzon

fraction addition and subtraction examples | Solidarios Con Garzon

Adding and Subtracting Mixed Numbers | Solidarios Con Garzon

Fraction Addition Subtraction Word Problems | Solidarios Con Garzon

Adding and subtracting fractions with unlike denominators | Solidarios Con Garzon

Free Adding And Subtracting Fractions Worksheets | Solidarios Con Garzon

Addition of Dissimilar Fractions | Solidarios Con Garzon

fraction addition and subtraction examples | Solidarios Con Garzon

Common Core Math Adding Fractions | Solidarios Con Garzon

How to Add Fractions with Different Denominators Step | Solidarios Con Garzon
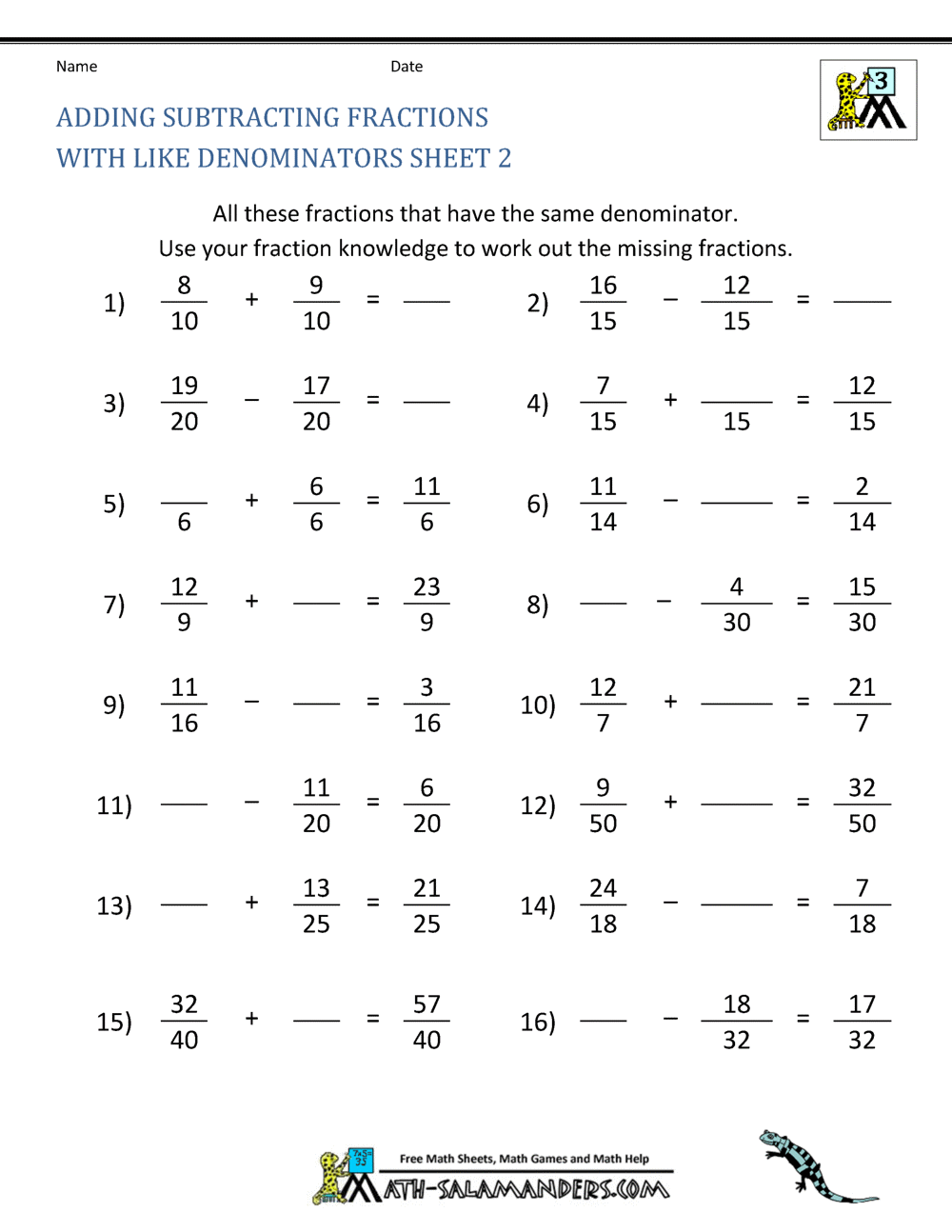
Worksheet On Addition And Subtraction Of Fractions | Solidarios Con Garzon

Show Me How To Add Fractions | Solidarios Con Garzon

Add And Subtract Unlike Fractions Calculator | Solidarios Con Garzon

Add Fractions Like A Pro With These Examples | Solidarios Con Garzon